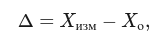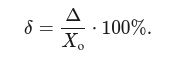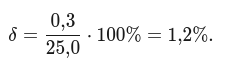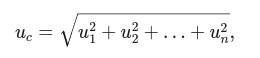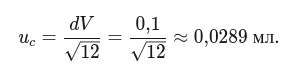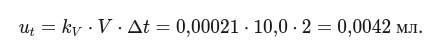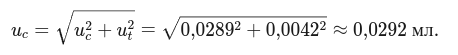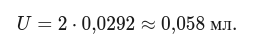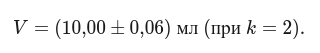Погрешность и неопределённость измерений

1. Основные понятия

Погрешность измерения — это разница между полученным в ходе измерения значением и истинным (или опорным) значением величины.

Ключевые особенности:

• всегда имеет конкретную величину и знак (может быть положительной или отрицательной);
• относится к конкретному результату, полученному определённым прибором или методом;
• предполагает, что истинное значение известно или может быть установлено.

Неопределённость измерения — количественная оценка того, насколько точно мы можем знать значение измеряемой величины. Это интервал, в пределах которого с заданной вероятностью может находиться истинное значение.

Ключевые особенности:

• не предполагает знания истинного значения — описывает лишь возможный разброс;
• учитывает все возможные источники ошибок и вариаций;
• выражается в виде диапазона значений вокруг измеренной величины.

2. Как рассчитывается погрешность

Абсолютная погрешность (Δ) показывает, на сколько единиц измерения результат отличается от истинного значения:

где:

• Xизм​ — результат измерения;
• Xо​ — опорное (истинное) значение.

Пример: если термометр показал 25,3 °C, а эталонный прибор зафиксировал 25,0 °C, то абсолютная погрешность составит:

Относительная погрешность (δ) выражает погрешность в процентах от истинного значения:

Для предыдущего примера:

3. Как оценивается неопределённость

Неопределённость учитывает все возможные источники вариаций, влияющие на результат. Её оценивают двумя основными методами:

Тип A (статистический):

• основан на повторных измерениях в одинаковых условиях;
• вычисляется через стандартное отклонение среднего значения;
• подходит для случайных погрешностей, проявляющихся при многократных измерениях.

Тип B (нестатистический):

• использует данные из документации приборов, калибровок, справочников;
• учитывает систематические погрешности, известные из опыта;
• применяется, когда многократные измерения невозможны или нецелесообразны.

Основные этапы оценки неопределённости:

1. Идентификация источников — выявление всех факторов, влияющих на результат (погрешности приборов, условия окружающей среды, человеческий фактор и т. д.).
2. Количественная оценка — присвоение каждому источнику численного значения неопределённости.
3. Комбинирование — объединение всех вкладов в суммарную стандартную неопределённость.
4. Расширение — расчёт интервала с заданным уровнем доверия.

4. Ключевые метрики неопределённости

Стандартная неопределённость ($u$) — оценка стандартного отклонения результата измерения. Показывает «типичное» отклонение от среднего значения.

Суммарная стандартная неопределённость (uc​) — объединённая неопределённость всех источников, рассчитанная по формуле:

где u1​,u2​,…,un​ — стандартные неопределённости отдельных источников.

Расширенная неопределённость ($U$) — интервал вокруг результата, в котором с высокой вероятностью находится истинное значение. Рассчитывается как:

где $k$ — коэффициент охвата (обычно 2 или 3).

Коэффициент охвата ($k$) зависит от:

• требуемого уровня доверия (например, 95 % или 99 %);
• типа распределения неопределённости (нормальное, прямоугольное и др.).

Для нормального распределения:

• $k=2$ соответствует уровню доверия ≈ 95 %;
• $k=3$ соответствует уровню доверия ≈ 99,7 %.

5. Практический пример расчёта неопределённости

Задача: измерить объём жидкости ($V$) с помощью бюретки с ценой деления 0,1 мл.

Источники неопределённости:

1. Погрешность считывания шкалы (uc​).
2. Влияние температуры (ut​).

Шаг 1. Неопределённость считывания (uc​)
Предполагаем прямоугольное распределение погрешности в пределах ± половины деления:

Шаг 2. Неопределённость из‑за температуры (ut​)
Допустим:

• измеренный объём $V=10,0\text{мл}$;
• колебания температуры $\Delta t=\pm 2°C$;
• коэффициент объёмного расширения воды kV​=0,00021 °C‾¹.

Тогда:

Шаг 3. Суммарная стандартная неопределённость (uc​)

Шаг 4. Расширенная неопределённость ($U$)
При $k=2$ (уровень доверия ≈ 95 %):

Итоговый результат:

Это означает, что истинный объём с вероятностью 95 % находится в интервале от 9,94 мл до 10,06 мл.

6. Сравнение погрешности и неопределённости

Критерий	Погрешность	Неопределённость
Суть	Отклонение от известного истинного значения	Оценка разброса возможных значений
Требование к истинному значению	Должно быть известно (или доступно для сравнения)	Не требует знания истинного значения
Фокус	На конкретном результате измерения	На всех возможных источниках вариаций
Форма выражения	Одно число (с знаком)	Интервал (диапазон значений)
Применение	В условиях, где можно сравнить с эталоном	В любых измерениях, включая сложные и косвенные