rcl-radio.ru

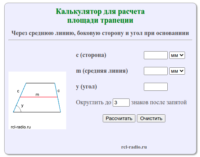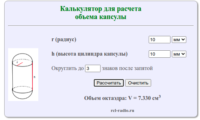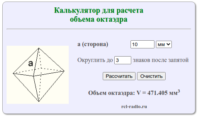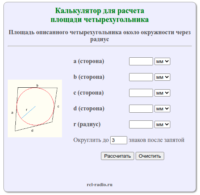
Ромб – четырёхугольник, у которого все стороны равны между собой. Ромб является частным случаем параллелограмма. Ромб с прямыми углами называется квадратом.  Формула для нахождения площади ромба через сторону и высоту: где: a — сторона ромба h — высота ромба  Формула для нахождения площади ромба через диагонали: где d1, d2 — диагонали ромба.  Формула […]

Трапеция — четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами. Средняя линия — отрезок, соединяющий середины боковых сторон.  Формула для нахождения площади трапеции через основания и высоту: где: a,b — основания трапеции h — высота трапеции  Формула […]

Шестиугольная призма — призма с шестиугольным основанием. У этого многогранника 8 граней, 18 рёбер и 12 вершин.  Формула для нахождения объема правильной шестиугольной призмы через сторону его граней (ребро) и высоту: где: a — сторона его граней (ребро) h — высота

 Формула расчета объёма прямого полого цилиндра через внутренний и наружный радиусы и высоту: где: R — наружный радиус r — внутренний радиус h — высота, π — 3,14  Формула расчета объёма прямого полого цилиндра через наружный диаметр, толщину стенки и высоту: где: D — наружный диаметр t — толщина стенки h — высота, […]

Капсула представляет собой базовую трехмерную геометрическую форму, состоящую из цилиндра с полусферическими концами. Другое название этой формы — сфероцилиндр. Форма используется для контейнеров для газов под давлением и для фармацевтических капсул.  Формула для нахождения объема капсулы: где: r — диаметр капсулы h — высота цилиндра капсулы

Октаэдр — правильный многогранник, составленный из 8 равносторонних треугольников.  Формула для нахождения объема октаэдра: где a — грань октаэдра.

Четырехугольник — это четырехугольная геометрическая фигура, образованная замкнутой ломаной линией, состоящей из четырех отрезков. Точки в четырехугольнике называются вершинами, отрезки называются сторонами или гранями четырехугольника.  Формула для нахождения площади четырехугольников через диагонали и угол между ними: где: d1 d2 — диагонали α — угол между диагоналями  Формула для нахождения площади четырехугольников через стороны и противолежащие углы: где: […]

Шестиугольник — многоугольник у которого все стороны равны, а все внутренние углы равны 120°. Формула для нахождения площади правильного шестиугольника через сторону: где a — сторона шестиугольника.  Формула для нахождения площади правильного шестиугольника через радиус описанной окружности:где r — радиус описанной окружности.  Формула для нахождения площади правильного шестиугольника через радиус вписанной окружности: где r […]

Эллипс — замкнутая кривая на плоскости, которая может быть получена как пересечение плоскости и кругового цилиндра или как ортогональная проекция окружности на плоскость. Формула для нахождения площади эллипса через полуоси: где: π — константа равная (3.14) a — малая полуось b — большая полуось

Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.  Формула нахождения площади треугольника с помощью половины его основания и высоту: где: a — основание треугольника h — высота треугольника  Формула Герона для нахождения площади треугольника: где: p — полупериметр треугольника a,b,c — стороны треугольника  Формула нахождения […]