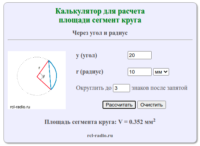
Сегмент круга, круговой сегмент — часть круга, ограниченная дугой окружности и её хордой или секущей. Формула для нахождения площади сегмента круга: где: π — константа равная (3.14) α — угол сегмента круга r — радиус окружности

Сегмент круга, круговой сегмент — часть круга, ограниченная дугой окружности и её хордой или секущей. Формула для нахождения площади сегмента круга: где: π — константа равная (3.14) α — угол сегмента круга r — радиус окружности
| Просмотров: 1 051 | Читать статью |
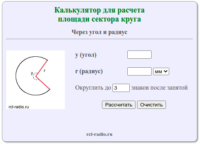
Сектор круга — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. Формула для нахождения площади сектора круга: где: l — длина дуги окружности r — радиус окружности Формула для нахождения площади сектора круга: где: π — константа равная (3.14) α — угол сектора круга r — радиус окружности
| Просмотров: 1 188 | Читать статью |
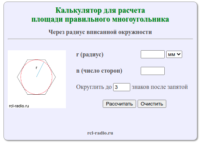
Многоугольник — геометрическая фигура, обычно определяемая как часть плоскости, ограниченная замкнутой ломаной. Если граничная ломаная не имеет точек самопересечения, многоугольник называется простым. Например, треугольники и квадраты — простые многоугольники, а пятиконечная звезда — нет. Вершины ломаной называются вершинами многоугольника, а её звенья — сторонами многоугольника. Число сторон многоугольника совпадает с числом его вершин. Формула […]
| Просмотров: 1 409 | Читать статью |
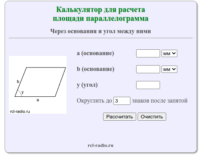
Параллелограмм — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб. Формула для нахождения площади прямоугольника через основание и высоту: где: a — длина основания h — высота Формула для нахождения площади прямоугольника через основания и угол между ними: где: a, […]
| Просмотров: 1 319 | Читать статью |