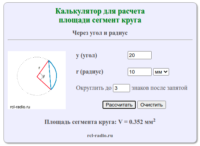
Сегмент круга, круговой сегмент — часть круга, ограниченная дугой окружности и её хордой или секущей. Формула для нахождения площади сегмента круга: где: π — константа равная (3.14) α — угол сегмента круга r — радиус окружности

Сегмент круга, круговой сегмент — часть круга, ограниченная дугой окружности и её хордой или секущей. Формула для нахождения площади сегмента круга: где: π — константа равная (3.14) α — угол сегмента круга r — радиус окружности
| Просмотров: 1 025 | Читать статью |
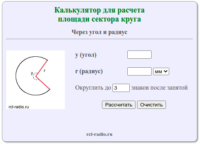
Сектор круга — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. Формула для нахождения площади сектора круга: где: l — длина дуги окружности r — радиус окружности Формула для нахождения площади сектора круга: где: π — константа равная (3.14) α — угол сектора круга r — радиус окружности
| Просмотров: 1 168 | Читать статью |
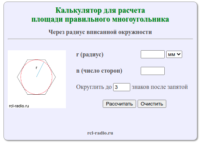
Многоугольник — геометрическая фигура, обычно определяемая как часть плоскости, ограниченная замкнутой ломаной. Если граничная ломаная не имеет точек самопересечения, многоугольник называется простым. Например, треугольники и квадраты — простые многоугольники, а пятиконечная звезда — нет. Вершины ломаной называются вершинами многоугольника, а её звенья — сторонами многоугольника. Число сторон многоугольника совпадает с числом его вершин. Формула […]
| Просмотров: 1 384 | Читать статью |
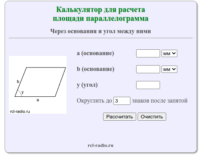
Параллелограмм — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб. Формула для нахождения площади прямоугольника через основание и высоту: где: a — длина основания h — высота Формула для нахождения площади прямоугольника через основания и угол между ними: где: a, […]
| Просмотров: 1 295 | Читать статью |
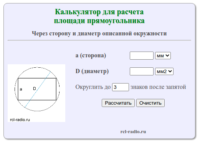
В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые, тогда четвёртый угол в силу теоремы о сумме углов многоугольника также будет равен 90°. В неевклидовой геометрии, где сумма углов четырёхугольника не равна 360°, прямоугольников не существует. Прямоугольник является параллелограммом — его противоположные стороны попарно параллельны. Диагонали любого прямоугольника […]
| Просмотров: 1 278 | Читать статью |
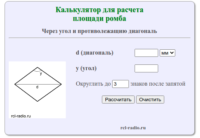
Ромб – четырёхугольник, у которого все стороны равны между собой. Ромб является частным случаем параллелограмма. Ромб с прямыми углами называется квадратом. Формула для нахождения площади ромба через сторону и высоту: где: a — сторона ромба h — высота ромба Формула для нахождения площади ромба через диагонали: где d1, d2 — диагонали ромба. Формула […]
| Просмотров: 1 346 | Читать статью |
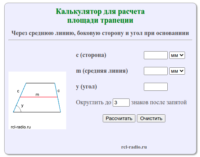
Трапеция — четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами. Средняя линия — отрезок, соединяющий середины боковых сторон. Формула для нахождения площади трапеции через основания и высоту: где: a,b — основания трапеции h — высота трапеции Формула […]
| Просмотров: 1 381 | Читать статью |
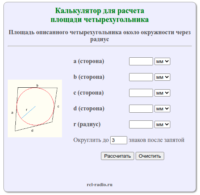
Четырехугольник — это четырехугольная геометрическая фигура, образованная замкнутой ломаной линией, состоящей из четырех отрезков. Точки в четырехугольнике называются вершинами, отрезки называются сторонами или гранями четырехугольника. Формула для нахождения площади четырехугольников через диагонали и угол между ними: где: d1 d2 — диагонали α — угол между диагоналями Формула для нахождения площади четырехугольников через стороны и противолежащие углы: где: […]
| Просмотров: 3 800 | Читать статью |

Шестиугольник — многоугольник у которого все стороны равны, а все внутренние углы равны 120°. Формула для нахождения площади правильного шестиугольника через сторону: где a — сторона шестиугольника. Формула для нахождения площади правильного шестиугольника через радиус описанной окружности:где r — радиус описанной окружности. Формула для нахождения площади правильного шестиугольника через радиус вписанной окружности: где r […]
| Просмотров: 1 962 | Читать статью |

Эллипс — замкнутая кривая на плоскости, которая может быть получена как пересечение плоскости и кругового цилиндра или как ортогональная проекция окружности на плоскость. Формула для нахождения площади эллипса через полуоси: где: π — константа равная (3.14) a — малая полуось b — большая полуось
| Просмотров: 1 204 | Читать статью |