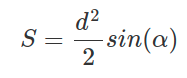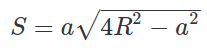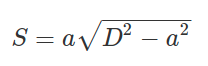В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые, тогда четвёртый угол в силу теоремы о сумме углов многоугольника также будет равен 90°. В неевклидовой геометрии, где сумма углов четырёхугольника не равна 360°, прямоугольников не существует.
- Прямоугольник является параллелограммом — его противоположные стороны попарно параллельны.
- Диагонали любого прямоугольника равны.
- Стороны прямоугольника являются его высотами. Середины сторон прямоугольника образуют ромб.
- Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (по теореме Пифагора).
- Около любого прямоугольника можно описать окружность, причём диагональ прямоугольника равна диаметру описанной окружности (радиус равен полудиагонали).
Формула для нахождения площади прямоугольника через стороны:
где a, b — стороны прямоугольника.
Формула для нахождения площади прямоугольника через диагонали и угол между ними:
где:
- d — диагональ
- α — угол между диагоналями
Формула для нахождения площади прямоугольника через диагональ и сторону:
где:
- a — сторона прямоугольника
- d — диагональ
Формула для нахождения площади прямоугольника через сторону и радиус описанной окружности:
где:
- a — сторона прямоугольника
- R — радиус описанной окружности
Формула для нахождения площади прямоугольника через сторону и диаметр описанной окружности:
где:
- a — сторона прямоугольника
- D — диаметр описанной окружности