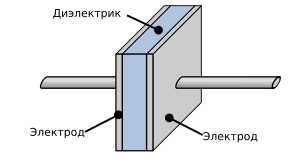
Авторство: Cepheiden, перевёл: Да будет цвет. Plate Capacitor DE.svg, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=138378329
Конденсатор — это устройство, способное накапливать электрический заряд и энергию. Его основными характеристиками являются емкость ($ C $) и напряжение ($ V $). Процесс зарядки и разрядки конденсатора связан с изменением электрического поля между его пластинами, что отражается в изменении величины заряда ($ Q $).
Зарядка конденсатора
При подключении источника постоянного напряжения ($ V $) к конденсатору через резистор ($ R $) начинается процесс зарядки. Ток ($ I $) в цепи определяется законом Ома:
$I = \frac{V}{R}$
Заряд ($ Q $) на пластинах конденсатора увеличивается со временем согласно уравнению:
$Q(t) = CV(1 — e^{-t/RC})$
где:
- $ t $ — время,
- $ R $ — сопротивление резистора,
- $ C $ — емкость конденсатора,
- $ e $ — основание натурального логарифма ($\approx 2.71828$),
- $ V $ — приложенное напряжение.
Со временем заряд достигает максимального значения $ Q_{\text{max}} = CV $, и ток стремится к нулю.
Постоянная времени
Важной характеристикой зарядки и разрядки конденсатора является постоянная времени ($ \tau $):
$\tau = RC$
Эта величина определяет, насколько быстро происходит изменение заряда. Через один интервал постоянной времени ($ t = \tau $) заряд достигает приблизительно $63\%$ от максимального значения.
Разрядка конденсатора
После отключения источника напряжения конденсатор начинает разряжаться через резистор. Напряжение ($ V(t) $) на конденсаторе убывает по экспоненте:
$V(t) = V_0 e^{-t/RC}$
где:
- $ V_0 $ — начальное напряжение на конденсаторе,
- $ t $ — время.
Соответственно, заряд ($ Q(t) $) также уменьшается:
$Q(t) = Q_0 e^{-t/RC}$
где:
- $ Q_0 $ — начальный заряд на конденсаторе.
Через каждый интервал постоянной времени заряд уменьшается на $63\%$.
Заключение
Процессы зарядки и разрядки конденсатора характеризуются экспоненциальными зависимостями от времени. Постоянная времени ($ \tau = RC $) играет ключевую роль в определении скорости этих процессов. Понимание этих явлений важно для проектирования электрических цепей и управления энергией в системах с использованием конденсаторов.
