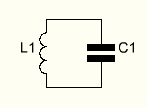
Колебательный контур — это электрическая цепь, состоящая из индуктивности ($L$) и ёмкости ($C$), которые соединены последовательно или параллельно. Основная функция такого контура заключается в накоплении энергии и её периодическом обмене между магнитным полем катушки индуктивности и электрическим полем конденсатора.
Последовательный колебательный контур
При подключении источника переменного напряжения к последовательному колебательному контуру ток в цепи будет зависеть от частоты входного сигнала. На определённой частоте, называемой резонансной частотой ($\omega_0$), полное сопротивление контура минимально, и амплитуда тока достигает максимума. Это явление называется резонансом. Резонансная частота определяется следующим образом:
$$\omega_0 = \frac{1}{\sqrt{LC}}$$
где:
- $\omega_0$ — угловая резонансная частота,
- $L$ — индуктивность катушки,
- $C$ — ёмкость конденсатора.
Частота резонанса в герцах ($f_0$) связана с угловой частотой через формулу:
$$f_0 = \frac{\omega_0}{2\pi}$$
Таким образом, при резонансе реактивные сопротивления индуктивности и ёмкости компенсируют друг друга, и контур ведёт себя как чисто активное сопротивление.
Параллельный колебательный контур
Параллельные контуры также демонстрируют резонанс, однако здесь максимальный ток достигается при минимальной проводимости цепи. В параллельных контурах резонанс наступает тогда, когда реактивные проводимости катушки и конденсатора равны. Угловая резонансная частота также определяется формулой:
$$\omega_0 = \frac{1}{\sqrt{LC}}$$
Математическое описание процессов
Рассмотрим процессы, происходящие в последовательном колебательном контуре.
Уравнения движения
Уравнение, описывающее изменение заряда на конденсаторе во времени, имеет вид:
$$\frac{d^2q(t)}{dt^2} + \frac{R}{L}\frac{dq(t)}{dt} + \frac{q(t)}{LC} = 0$$
где:
- $q(t)$ — заряд на конденсаторе,
- $R$ — сопротивление контура,
- $L$ — индуктивность,
- $C$ — ёмкость.
Это уравнение является дифференциальным уравнением второго порядка, которое описывает гармонические колебания системы. Решение этого уравнения зависит от значения коэффициента затухания ($\gamma = R/2L$) и собственной частоты ($\omega_0$). Если коэффициент затухания меньше собственной частоты ($\gamma < \omega_0$), система совершает затухающие колебания.
Затухание колебаний
Амплитуда колебаний уменьшается экспоненциально со временем:
$$A(t) = A_0 e^{-\gamma t}$$
где:
- $A_0$ — начальная амплитуда,
- $\gamma$ — коэффициент затухания.
Время релаксации ($\tau$) — время, за которое амплитуда уменьшается в $e$ раз, определяется как:
$$\tau = \frac{1}{\gamma} = \frac{2L}{R}$$
Комплексное сопротивление (импеданс) колебательного контура
Импеданс ($Z$) колебательного контура — это комплексное сопротивление, которое учитывает как активные, так и реактивные компоненты. Для последовательного контура импеданс определяется как:
$$Z = R + j\left(\omega L — \frac{1}{\omega C}\right)$$
где:
- $j$ — мнимая единица,
- $\omega$ — угловая частота входного сигнала.
Реактивная составляющая импеданса обусловлена индуктивностью и ёмкостью. При резонансе реактивные составляющие компенсируются, и импеданс становится минимальным.
Для параллельного контура импеданс выражается через проводимость:
$$Y = \frac{1}{R} + j\left(\omega C — \frac{1}{\omega L}\right)$$
Импеданс играет важную роль в анализе электрических цепей, особенно при расчёте характеристик фильтров и усилителей.
Колебательные контуры широко используются в радиотехнике, электронике и телекоммуникациях благодаря своей способности селективно усиливать или ослаблять сигналы определённых частот. Понимание принципов работы и математического описания процессов позволяет проектировать эффективные схемы и устройства.