rcl-radio.ru

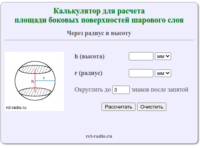
Шаровой слой — часть шара, ограниченная двумя параллельными плоскостями, пересекающими шар. Основания шарового слоя — это сечения шара, образовавшиеся в результате пересечения шара двумя параллельными плоскостями. Высота шарового слоя — это расстояние между основаниями слоя.  Формула для расчета площади боковых поверхностей шарового слоя: где: r — радиус шара h — высота шарового слоя π […]

Квадрат — правильный четырёхугольник, у которого все стороны и углы равны между собой. У квадрата есть две диагонали, соединяющие не смежные вершины. Квадрат является частным случаем прямоугольника, ромба и параллелограмма.  Формула для нахождения площади квадрата через сторону: где a — сторона квадрата.  Формула для нахождения площади квадрата через диагональ: где D — диагональ квадрата.

Кольцо — плоская геометрическая фигура, ограниченная двумя концентрическими окружностями. Площадь кольца, ограниченного окружностями радиусов R и r, определяется как разность площадей кругов с такими радиусами: Площадь кольца также может быть вычислена путём умножения числа пи на квадрат половины длины самого большого отрезка, лежащего внутри кольца. Это можно доказать через теорему Пифагора — такой отрезок будет […]

Сектор кольца — это часть круга, ограниченная дугами разных радиусов, проведенных из одной точки — центра, и двумя радиусами, проведенными к концам дуги большего радиуса.  Формула для нахождения площади сектора кольца: где: π — константа равная (3.14) α — угол сегмента круга r1 — радиус внешней окружности r2 — радиус внутренней окружности.

Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга). Формула для нахождения площади круга через радиус: где: π — константа равная (3.14) r — радиус круга  Формула для нахождения площади круга через диаметр: где: π — константа равная (3.14) D — диаметр  Формула […]

Сегмент круга, круговой сегмент — часть круга, ограниченная дугой окружности и её хордой или секущей.  Формула для нахождения площади сегмента круга: где: π — константа равная (3.14) α — угол сегмента круга r — радиус окружности

Сектор круга — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. Формула для нахождения площади сектора круга: где: l — длина дуги окружности r — радиус окружности Формула для нахождения площади сектора круга: где: π — константа равная (3.14) α — угол сектора круга r — радиус окружности

Многоугольник — геометрическая фигура, обычно определяемая как часть плоскости, ограниченная замкнутой ломаной. Если граничная ломаная не имеет точек самопересечения, многоугольник называется простым. Например, треугольники и квадраты — простые многоугольники, а пятиконечная звезда — нет. Вершины ломаной называются вершинами многоугольника, а её звенья — сторонами многоугольника. Число сторон многоугольника совпадает с числом его вершин.  Формула […]

Параллелограмм — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.  Формула для нахождения площади прямоугольника через основание и высоту: где: a — длина основания h — высота  Формула для нахождения площади прямоугольника через основания и угол между ними: где: a, […]

В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые, тогда четвёртый угол в силу теоремы о сумме углов многоугольника также будет равен 90°. В неевклидовой геометрии, где сумма углов четырёхугольника не равна 360°, прямоугольников не существует. Прямоугольник является параллелограммом — его противоположные стороны попарно параллельны. Диагонали любого прямоугольника […]