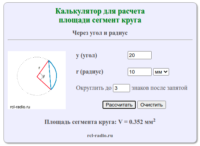
Сегмент круга, круговой сегмент — часть круга, ограниченная дугой окружности и её хордой или секущей. Формула для нахождения площади сегмента круга: где: π — константа равная (3.14) α — угол сегмента круга r — радиус окружности

Сегмент круга, круговой сегмент — часть круга, ограниченная дугой окружности и её хордой или секущей. Формула для нахождения площади сегмента круга: где: π — константа равная (3.14) α — угол сегмента круга r — радиус окружности
| Просмотров: 1 027 | Читать статью |
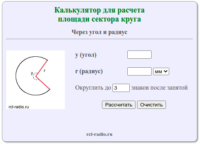
Сектор круга — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. Формула для нахождения площади сектора круга: где: l — длина дуги окружности r — радиус окружности Формула для нахождения площади сектора круга: где: π — константа равная (3.14) α — угол сектора круга r — радиус окружности
| Просмотров: 1 171 | Читать статью |
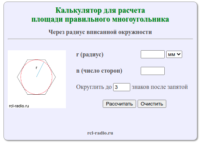
Многоугольник — геометрическая фигура, обычно определяемая как часть плоскости, ограниченная замкнутой ломаной. Если граничная ломаная не имеет точек самопересечения, многоугольник называется простым. Например, треугольники и квадраты — простые многоугольники, а пятиконечная звезда — нет. Вершины ломаной называются вершинами многоугольника, а её звенья — сторонами многоугольника. Число сторон многоугольника совпадает с числом его вершин. Формула […]
| Просмотров: 1 389 | Читать статью |
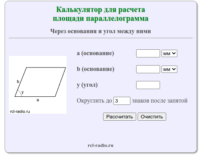
Параллелограмм — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб. Формула для нахождения площади прямоугольника через основание и высоту: где: a — длина основания h — высота Формула для нахождения площади прямоугольника через основания и угол между ними: где: a, […]
| Просмотров: 1 300 | Читать статью |
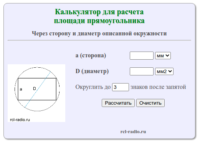
В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые, тогда четвёртый угол в силу теоремы о сумме углов многоугольника также будет равен 90°. В неевклидовой геометрии, где сумма углов четырёхугольника не равна 360°, прямоугольников не существует. Прямоугольник является параллелограммом — его противоположные стороны попарно параллельны. Диагонали любого прямоугольника […]
| Просмотров: 1 283 | Читать статью |
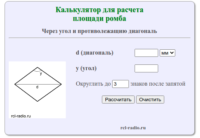
Ромб – четырёхугольник, у которого все стороны равны между собой. Ромб является частным случаем параллелограмма. Ромб с прямыми углами называется квадратом. Формула для нахождения площади ромба через сторону и высоту: где: a — сторона ромба h — высота ромба Формула для нахождения площади ромба через диагонали: где d1, d2 — диагонали ромба. Формула […]
| Просмотров: 1 349 | Читать статью |
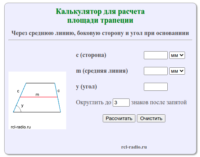
Трапеция — четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами. Средняя линия — отрезок, соединяющий середины боковых сторон. Формула для нахождения площади трапеции через основания и высоту: где: a,b — основания трапеции h — высота трапеции Формула […]
| Просмотров: 1 384 | Читать статью |

Шестиугольная призма — призма с шестиугольным основанием. У этого многогранника 8 граней, 18 рёбер и 12 вершин. Формула для нахождения объема правильной шестиугольной призмы через сторону его граней (ребро) и высоту: где: a — сторона его граней (ребро) h — высота
| Просмотров: 2 838 | Читать статью |

Формула расчета объёма прямого полого цилиндра через внутренний и наружный радиусы и высоту: где: R — наружный радиус r — внутренний радиус h — высота, π — 3,14 Формула расчета объёма прямого полого цилиндра через наружный диаметр, толщину стенки и высоту: где: D — наружный диаметр t — толщина стенки h — высота, […]
| Просмотров: 5 921 | Читать статью |
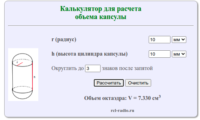
Капсула представляет собой базовую трехмерную геометрическую форму, состоящую из цилиндра с полусферическими концами. Другое название этой формы — сфероцилиндр. Форма используется для контейнеров для газов под давлением и для фармацевтических капсул. Формула для нахождения объема капсулы: где: r — диаметр капсулы h — высота цилиндра капсулы
| Просмотров: 2 257 | Читать статью |