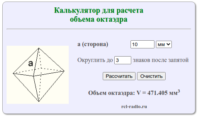
Октаэдр — правильный многогранник, составленный из 8 равносторонних треугольников. Формула для нахождения объема октаэдра: где a — грань октаэдра.

Октаэдр — правильный многогранник, составленный из 8 равносторонних треугольников. Формула для нахождения объема октаэдра: где a — грань октаэдра.
| Просмотров: 2 037 | Читать статью |
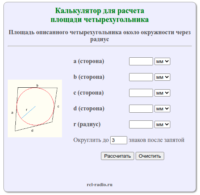
Четырехугольник — это четырехугольная геометрическая фигура, образованная замкнутой ломаной линией, состоящей из четырех отрезков. Точки в четырехугольнике называются вершинами, отрезки называются сторонами или гранями четырехугольника. Формула для нахождения площади четырехугольников через диагонали и угол между ними: где: d1 d2 — диагонали α — угол между диагоналями Формула для нахождения площади четырехугольников через стороны и противолежащие углы: где: […]
| Просмотров: 3 825 | Читать статью |

Шестиугольник — многоугольник у которого все стороны равны, а все внутренние углы равны 120°. Формула для нахождения площади правильного шестиугольника через сторону: где a — сторона шестиугольника. Формула для нахождения площади правильного шестиугольника через радиус описанной окружности:где r — радиус описанной окружности. Формула для нахождения площади правильного шестиугольника через радиус вписанной окружности: где r […]
| Просмотров: 1 980 | Читать статью |

Эллипс — замкнутая кривая на плоскости, которая может быть получена как пересечение плоскости и кругового цилиндра или как ортогональная проекция окружности на плоскость. Формула для нахождения площади эллипса через полуоси: где: π — константа равная (3.14) a — малая полуось b — большая полуось
| Просмотров: 1 207 | Читать статью |

Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Формула нахождения площади треугольника с помощью половины его основания и высоту: где: a — основание треугольника h — высота треугольника Формула Герона для нахождения площади треугольника: где: p — полупериметр треугольника a,b,c — стороны треугольника Формула нахождения […]
| Просмотров: 1 316 | Читать статью |

Усечённая пирамида — часть пирамиды, заключенная между её основанием, боковыми гранями и сечением этой пирамиды плоскостью, параллельной основанию. Формула объема усеченной пирамиды через высоту и площадь основания: где: S1 — площадь верхнего основания S2 — площадь нижнего основания h — высота усеченной пирамиды
| Просмотров: 2 125 | Читать статью |

Пирамида Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину. Пирамида является частным случаем конуса. Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания. Формула объема пирамиды через высоту и площадь основания: где: S — площадь основания h — высота пирамиды Правильная пирамида Правильная […]
| Просмотров: 2 052 | Читать статью |

Куб — правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра и грани куба равны. Формула объема куба: где: a — ребро куба
| Просмотров: 1 746 | Читать статью |
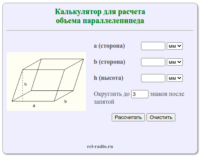
Параллелепипед — многогранник, у которого шесть граней и каждая из них параллелограмм. Объем параллелепипеда равен произведению его длины, ширины и высоты. где: a — длина стороны прямоугольного параллелепипеда b — длина стороны прямоугольного параллелепипеда h — высота прямоугольного параллелепипеда
| Просмотров: 1 923 | Читать статью |

Параллелепипед — многогранник, у которого шесть граней и каждая из них параллелограмм. Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники. Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты. где: a — длина прямоугольного параллелепипеда b — ширина прямоугольного параллелепипеда с — высота прямоугольного параллелепипеда
| Просмотров: 2 078 | Читать статью |