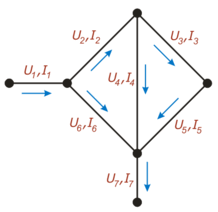
1. Формулировка правил (законов)
1.1. Определения
Ток — это поток зарядов через проводник, который измеряется в амперах (А).
Напряжение — разность потенциалов между двумя точками в электрической цепи, измеряемая в вольтах (В).
Узел — точка соединения трёх или более ветвей электрической цепи.
Контур — замкнутый путь в электрической цепи, проходящий через несколько узлов.
1.2. Первое правило
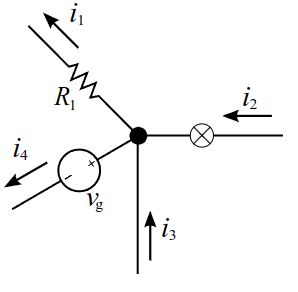
Авторство: KCL.png: Pflododerivative work: M0tty (talk). KCL.png, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=16594174
Первое правило Киргофа гласит, что алгебраическая сумма всех токов, входящих в узел и выходящих из узла, равна нулю. Это означает, что суммарный ток, приходящий в узел, равен суммарному току, уходящему из узла.
Математически это выражается следующим образом:
$ \sum_{k=1}^{n} I_k = 0$
где $I_k$ — токи, входящие в узел ($I_k > 0$) или выходящие из узла ($I_k < 0$), а $n$ — общее количество ветвей, соединённых с узлом.
1.3. Второе правило
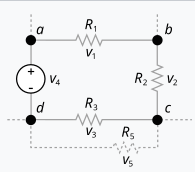
Авторство: Kwinkunks. Собственная работа, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=11056469
Второе правило Киргофа утверждает, что алгебраическая сумма падений напряжений вдоль любого замкнутого контура электрической цепи равна нулю. Иными словами, сумма ЭДС (электродвижущих сил), действующих в контуре, равна сумме падений напряжений на сопротивлениях этого же контура.
Математическое выражение второго закона выглядит так:
$ \sum_{k=1}^{m} V_k = 0$
где $V_k$ — падения напряжений на элементах цепи, а $m$ — количество элементов в контуре.
2. Уравнения для токов и напряжений
Общественное достояние, https://commons.wikimedia.org/w/index.php?curid=620221
Используя оба правила Киргофа, можно составить систему уравнений для расчёта токов и напряжений в сложной электрической схеме. Эта система уравнений строится на основе законов Ома и Киргофа.
Например, для простой схемы с одним источником ЭДС и несколькими резисторами можно записать следующие уравнения:
$ \begin{cases}
I_1 + I_2 + I_3 = 0 & \text{(первое правило)} \\
E_1 — R_1 I_1 — R_2 I_2 = 0 & \text{(второе правило)}
\end{cases}$
Решив эту систему, можно найти значения токов и напряжений.
3. Пример
Рассмотрим схему с двумя источниками ЭДС и тремя резисторами:
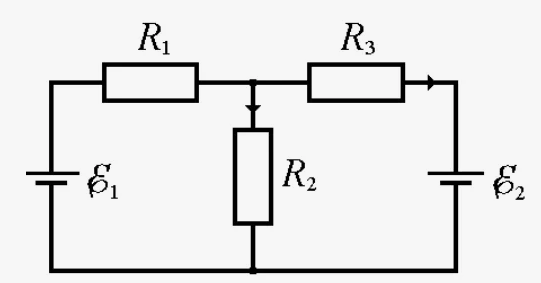
Применяя первое и второе правила Киргофа, получаем следующую систему уравнений:
$ \begin{cases}
I_1 — I_2 — I_3 = 0 & \text{(узел A)} \\
E_1 — R_1 I_1 — E_2 + R_2 I_2 = 0 & \text{(контур ABCDA)} \\
R_2 I_2 + R_3 I_3 = 0 & \text{(контур BCDB)}
\end{cases}$
Решение этой системы даёт значения токов $I_1$, $I_2$ и $I_3$.
4. О значении для электротехники
Законы Киргофа играют ключевую роль в анализе электрических цепей, позволяя инженерам и учёным разрабатывать и моделировать различные схемы. Они применяются в проектировании электронных устройств, разработке энергетических систем и оптимизации потребления электроэнергии.
5. Значение в математике
Законы Киргофа имеют аналогии в линейной алгебре и теории графов. Например, первое правило соответствует закону сохранения заряда, а второе — принципу потенциальности электрического поля. Эти принципы широко используются в численных методах решения систем уравнений.
6. Другие законы, открытые Кирхгофом
Густав Роберт Кирхгоф внёс значительный вклад в физику, открыв несколько важных законов помимо тех, что касаются электрических цепей.
6.1. Закон излучения Кирхгофа
Этот закон устанавливает связь между способностью тела поглощать и излучать электромагнитные волны. Согласно этому закону, отношение спектральной плотности энергетической яркости абсолютно чёрного тела к его спектральной поглощательной способности одинаково для всех тел при данной температуре и равно спектральной плотности энергетической яркости абсолютно чёрного тела.
6.2. Закон Кирхгофа в химии
Закон Кирхгофа в термодинамике гласит, что температурный коэффициент теплового эффекта химической реакции равен изменению изобарного потенциала реакции при изменении температуры. Этот закон помогает предсказывать изменение тепловых эффектов реакций при разных температурах.
—
Таким образом, законы Киргофа охватывают широкий спектр научных дисциплин, от электротехники до математики и химии, и продолжают оставаться важными инструментами для анализа и разработки современных технологий.
Загрузка...