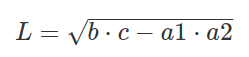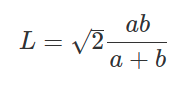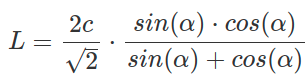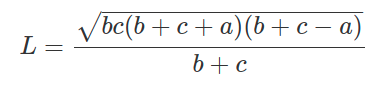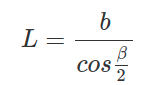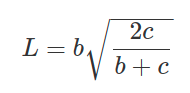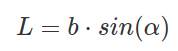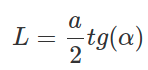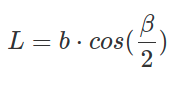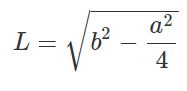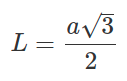Биссектриса — луч, исходящий из вершины угла и делящий этот угол на два равных угла. Можно также определить биссектрису как геометрическое место точек внутри угла, равноудалённых от сторон этого угла.
Биссектрисой треугольника называется отрезок биссектрисы угла, проведенный от вершины угла до её пересечения с противолежащей стороной. У треугольника существуют три биссектрисы, соответствующие трём его вершинам.
Формула для расчета длины биссектрисы в треугольнике через стороны и отрезки:
Где: b, c — стороны, a1, a2 — длины отрезков, образованных на стороне
Формула для расчета длины биссектрисы в треугольнике через катеты:
Где: a, b — катеты
Формула для расчета длины биссектрисы в треугольнике через гипотенузу и угол:
Где: c — гипотенуза, sin α, cos α — угол
Формула для расчета длины биссектрисы в треугольнике через две стороны и угол между ними:
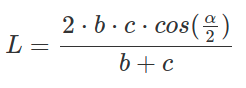Где: b, c — стороны, cos α — угол между сторонами
Формула для расчета длины биссектрисы в треугольнике через все стороны:
Где: a, b, c — стороны
Формула для расчета длины биссектрисы из острого угла в прямоугольном треугольнике через катет и угол:
Где: b — катет, cos β — угол
Формула для расчета длины биссектрисы из острого угла в прямоугольном треугольнике через катет и гипотенузу:
Где: b — катет, c — гипотенуза
Формула для расчета длины биссектрисы в равнобедренном треугольнике через боковую сторону и угол при основании:
Где: b — боковая сторона, sin α — угол при основании
Формула для расчета длины биссектрисы в равнобедренном треугольнике через основание и угол при основании:
Где: a — основание, tg α — угол при нижнем основании
Формула для расчета длины биссектрисы в равнобедренном треугольнике через боковую сторону и угол между боковыми сторонами:
Где: b — боковая сторона, cos β — угол между боковыми сторонами
Формула для расчета длины биссектрисы в равнобедренном треугольнике через основание и боковую сторону:
Где: b — боковая сторона, a — основание
Формула для расчета длины биссектрисы в равностороннем треугольнике через сторону:
Где: a — сторона
Загрузка...